महत्तम और लघुत्तम समापवर्त्य

भिन्नों का महत्तम समापवर्तक और लघुत्तम समापवर्त्य

1. दी गई भिन्नों का महत्तम समापवर्तक

उदाहरण: 1/2 और 3/4 का महत्तम समापवर्तक

2. दी गई भिन्नों का लघुत्तम समापवर्त्य

उदाहरण: 1/2 और 3/4 का लघुत्तम समापवर्त्य

दो संख्याओं का गुणनफल = (उन संख्याओं का HCF) × (उन संख्याओं का LCM)

गुणक और गुणजः   यदि एक संख्या ‘x’ दूसरी संख्या ‘y’ को पूर्णतः विभाजित करती है तो हम ‘x’ को ‘y’ का गुणक कहते हैं। इस अवस्था में ‘y’, ‘x’ का गुणज कहलाता है।

गुणनखण्डः   जब कोई संख्या किसी दूसरी संख्या को पूरा-पूरा विभाजित करे और शेष कुछ न बचे तो वह संख्या उस दूसरी संख्या का गुणनखण्ड कहलाती है।

जैसे- संख्या 15, 3 और 5 से पूरी-पूरी विभाजित हो जाती है। अतः 3 और 5, 15 के गुणनखण्ड हैं।

महत्तम समापवर्तक (HCF)

दो या दो से अधिक संख्या का महत्तम समापवर्तक वह बड़ी से बड़ी संख्या होती है, जो प्रत्येक दी गई संख्याओं को पूरा-पूरा विभाजित कर सके। चलिए जानते हैं विस्तार से। 

महत्तम समापवर्तक हम निम्नलिखित दो विधियों द्वारा ज्ञात कर सकते हैं:

1. अभाज्य गुणनखण्ड विधि

उदाहरण: 144, 180 और 108 का महत्तम समापवर्तक इस विधि द्वारा निम्न प्रकार ज्ञात कर सकते हैं –

• 144 = 2 × 2 × 3 × 3 × 2 ×2
• 108 = 2 × 2 × 3 × 3 × 3
• 180 = 2 × 2 × 3 × 3 × 5

उपरोक्त तीनों संख्याओं के अभाज्य गुणनखण्डों में उभयनिष्ठ 

गुणनखण्ड यानी जो तीनों में शामिल है । चूँकि 144,  108, 180 के गुणनखण्ड में 2 × 2 × 3 × 3  उभयनिष्ठ( समान या common)  है।   2 × 2 × 3 × 3 = 36 

∴ 144, 180 और 108 का अभीष्ट महत्तम समापवर्तक 36 होगा। इसी प्रकार हम सभी संख्याओं का म.स.( महत्तम समापवर्तक) निकाल सकते हैं।

2. भाग विधि

  
यह विधि निम्नलिखित शर्तों पर आधारित है -

• इस विधि में हम उस संख्या से भाग करते हैं जो छोटी हो। 
• भाग करने पर जो शेषफल आता है उस संख्या से उस संख्या में भाग करते हैं जिससे कि ये शेषफल प्राप्त हुआ था। 
• अब जो संख्याएँ बचीं है उनमें से छोटी संख्या लेकर बडी़ संख्या में भाग करीए बिल्कुल पहले की भाँति। 
• अब अन्त में ये देखिए कि कौन सी वह संख्या है जो सबको पूरी तरह से विभाजित कर रही है। 
• यही संख्या महत्तम समापवर्तक है। 

चलिए उदाहरण देखते हैं ः-

उदाहरण: उपरोक्त संख्याओं का महत्तम समापवर्तक भाग विधि द्वारा निम्न प्रकार ज्ञात कर सकते हैं –

                               

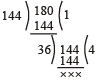
अब 36 और 108 का महत्तम समापवर्तक ज्ञात करना है।

   

                                

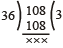
अतः 144,180 और 108 का महत्तम समापवर्तक 36 होगा।


नोट :-     संख्याओं 144,180 और 108 में 108 और 144 दोनों 180 से छोटी हैं अतः हम 144 के स्थान पर 108 से भी भाग कर सकते हैं।

              बहुपदों का महत्तम समापवर्तक 

( Highest Common Factor of Polynomials  ) 

उदाहरण   1.  x² - 4      तथा      x - 2  का महत्तम समापवर्तक ज्ञात किजिए : 


हल :   x² - 4     और   x - 2 का गुणनखण्ड करने पर,

x² - 4 = ( x - 2  ) (   x + 2  )   तथा 

  x - 2 = ( x - 2  ) × 1

दोनों में  ( x - 2  ) कामन है अथवा  ( x - 2  ) दोनोंगुणनखण्ड  को पूरा - पूरा विभाजित करने वाली एकमात्र गुणनखण्ड है। जो दोनों में मिल रहा है । अतः x² - 4     और   x - 2 का महत्तम समापवर्तक   x - 2 है।

उदाहरण   2.   x³ - 8    तथा    x² - 10x + 16 का महत्तम समापवर्तक ज्ञात किजिए  । 

हल : दोनों व्यजंको  x³ - 8   और   x² - 10x + 16 का 

 गुणनखण्ड करने पर, 
                               x³ - 8 = ( x - 2 ) ( x² + 2x + 4 ) 

तथा            x² - 10x + 16 =   x² - 2x  -  8x + 16 

                  x² - 10x + 16 =   x ( x - 2 ) - 8 ( x - 2 ) 
                  x² - 10x + 16 =   ( x - 2 )  ( x - 8 ) 

दोनों व्यजंको में मिलने वाला  ( x - 2 )  गुणनखण्ड है।

अतः इनका महत्तम समापवर्तक ( x - 2 ) है।

                *  📓भिन्न की जानकारी
                * ⚡ mind-update करना।


         

लघुत्तम समापवर्त्य (LCM)

दो या दो से अधिक दी गई संख्याओं का लघुत्तम समापवर्त्य वह छोटी से छोटी संख्या होती है जो प्रत्येक दी गई संख्या से पूरी-पूरी विभाजित हो सके।

लघुत्तम समापवर्त्य हम निम्नलिखित दो विधियों द्वारा ज्ञात कर सकते हैं:

1. अभाज्य गुणनखण्ड विधि

उदाहरण: 12, 16 तथा 30 का लघुत्तम समापवर्त्य इस विधि द्वारा निम्न प्रकार ज्ञात कर सकते हैं-

• 12 = 2 × 2 × 3
• 16 = 2 × 2 × 2 × 2
• 30 = 2 × 3 × 5

अब तीनों संख्याओं के अभाज्य गुणनखंडों में 2 सबसे अधिक 4 बार तथा 3 एक बार और 5 एक बार आया है।

इस प्रकार दी गई संख्याओं का अभीष्ट लघुत्तम समापवर्त्य
= 2 × 2 × 2 × 2 × 3 × 5 = 240 होगा।

परीक्षणः  अब हमका परीक्षण करेंगे कि क्या ये 240 संख्याओं 12,  16,  30 से पूरी तरह विभाजित होती है। 

240 ÷ 12 = 20

240 ÷ 16 = 15

240 ÷ 30 = 4

चूँकि पूरी तरह विभाजित हो रहीं हैं अतः ये उत्तर सही(✅) है।

2. भाग विधि

उदाहरण: उपरोक्त संख्याओं का लघुत्तम समापवर्त्य भाग विधि द्वारा इस प्रकार ज्ञात करेंगे:

• सबसे पहले सभी संख्याओं को a, b, c, d क्रम में रख लेंते हैं। 
• अब इनमें उस छोटी संख्या से भाग करते हैं जिससे कि भाग पूरी तरह से चली जाये। 
• भाग जितनी बार जाती है उस अंक को उस संख्या के निचे लिखें। 
• छोटी संख्या से तब तक करें जब तक कि इन संख्याओं का भागफल, 1 न हो जाए। 
• अब जिन -  जिन संख्याओं से भाग किया गया है उन सभी का आपस में गुणा कर दीजिए। यही है ल.स.(लघुत्तम समापवर्त्य)

चलिए उदाहरण पर नज़र डालते हैं -

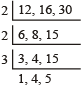
∴ दी गई संख्याओं का अभीष्ट लघुत्तम समापवर्त्य

= 2 × 2 × 3 × 1 × 4 × 5 = 240 होगा।

भिन्नों का महत्तम समापवर्तक और लघुत्तम समापवर्त्य के सूत्र : 

1. दी गई भिन्नों का महत्तम समापवर्तक

उदाहरण: 1/2 और 3/4 का महत्तम समापवर्तक

2. दी गई भिन्नों का लघुत्तम समापवर्त्य

उदाहरण: 1/2 और 3/4 का लघुत्तम समापवर्त्य

दो संख्याओं का गुणनफल = (उन संख्याओं का HCF) × (उन संख्याओं का LCM)

भिन्न जैसी आवश्यक जानकारी हमे होनी चाहिए। इसलिए आपको भिन्न के महत्तम समापवर्तक और लघुत्तम समीपवर्तक  के लिए सूत्र दी जा रही है ताकि आप ऊपर बताए गए उदाहरणों की सहायता से आप हल कर सको।  आपका कीमती समय बचे इसलिए हम अब यहीं विराम देते हैं । 

अगर आपको कोई समस्या होती है इसको हल करने में तो आपकी मदत करने की पूरी कोशिश की जायेगी । जो भी सवाल हो हमें कमेन्ट करके जरूर पूँछ हमें आपकी सहायता करने में बहुत प्रशन्नता होगी। 

Thanks for Reading............. 

---